Turunan

TURUNAN

Turunan dalam ilmu kalkulus merupakan pengukuran terhadap bagaimana fungsi berubah seiring perubahan nilai input. Secara umum, turunan menyatakan bagaimana suatu besaran berubah akibat perubahan besaran lainnya; contohnya, turunan dari posisi sebuah benda bergerak terhadap waktu adalah kecepatan sesaat objek tersebut.

Proses dalam menemukan turunan disebut diferensiasi. Kebalikan dari turunan disebut dengan antiturunan. Teorema fundamental kalkulus mengatakan bahwa antiturunan sama dengan integrasi. Turunan dan integral adalah 2 fungsi penting dalam kalkulus.

• ${\displaystyle (\ln x)'={\frac {1}{x}}\,}$
• ${\displaystyle (\sin x)'=\cos x\,}$
• ${\displaystyle (\cos x)'=-\sin x\,}$
• ${\displaystyle (\tan x)'=\sec ^{2}x\,}$

• ${\displaystyle y'}$ adalah simbol untuk turunan pertama.
• ${\displaystyle y''}$ adalah simbol untuk turunan kedua.
• ${\displaystyle y'''}$ adalah simbol untuk turunan ketiga.

simbol lainnya selain ${\displaystyle y'\,}$ dan ${\displaystyle y''\,}$ adalah ${\displaystyle {\frac {dy}{dx}}\,}$ dan ${\displaystyle {\frac {d^{2}y}{(dx)^{2}}}\,}$

1.  Turunan Pertama

Rumus :

y = Cxⁿ

ket : C & ⁿ = Konstanta Real

contoh :

^·          y = 4x⁴², maka dy/dx =  4.2x ^2-1 = 8x

^·          y = x² + 2x² , maka dy/dx = 2x+ 4

2.   Turunan Kedua

Turunan kedua dinotasikan sebagai berikut :

d²y/d²x atau y’’

Turunan kedua merupakan turunan yang diperoleh dengan menurunkan kembali turunan pertama. Perhatikan contoh berikut :

y = x³+ x⁴ + x + 2

dy/dx = 3x² + 4x + 1

d²y/d²x = 6x + 4

3.  Turunan Trigonometri

Berikut rumus turunan fungsi Trigonometri :

a)     f (x) = sin x , maka f ‘ (x) = cos x

b)    f (x) = cos x , maka f ‘ (x) = - sin x

c)     f ‘ (x) = sec²x = 1/cos²x

perhatikan contoh berikut :

            jika y = x² sin 2x , maka dy/dx ?

            jawab :

                        y = x² sin 2x

                        misalkan :

                        u(x) = x² , maka u’(x) = 2x

                        v(x) = sin2x , maka v’(x) = 2 cos 2x

                        y = u(x) . v(x)

                        y ‘ (x) = u’(x)v(x) + u(x) v’(x)

INTEGRAL

Integral merupakan kebalikan dari turunan. Jika F(x) adalah fungs umum yang bersifat F(x) = f(x), maka F(x) merupakan anti turunan atau integral dari f(x). Pengintegralan fungsi f(x) terhadap x dinotasikan sebagai berikut :

                        ∫ f(x) dx = F(x) + C

                        Keterangan :

                        ∫ = notasi integral

                        f(x) = fungsi integral

                        F(x) = fungsi integral umum yang bersifat F(x) = f(x)

                        C = Konstanta

1     Integral tak tentu

  Rumus Dasar :

a)     ∫ a dx = ax + c

b)    ∫ xⁿ dx = 1/n+1 xⁿ⁺¹ + C dengan catatan n ≠ -1

c)     Integral Tak Tentu Fungsi Trigonometri

§  ∫ sin x dx = - cos x + C

§  ∫ cos x dx = - sin x + C

Contoh :  Tentukan nilai dari ʃ 4 sin x + 7 cos x dx !

penyelsaian:

ʃ sin x dx = – cos x + C
ʃ cos x dx = sin x + C
Maka:
ʃ 4 sin x + 7 cos x dx = – 4cos x + 7sin x + C
Jadi, nilai dari nilai dari ʃ 4 sin x + 7 cos x dx adalah – 4cos x + 7sin x + C.

2     Integral Tentu     

      Integral Tentu adalah integral dengan batas-batas yang sudah di tentukan, dengan dinotasikan sebagai berikut :

 ∫^b_a  f(x) dx = [F(x)]^b_a = F(b) – F(a)

Keterangan : A dan b adalah batas bawah integral dan batas atas integral.

   Contoh : Carilah hasil dari ʃ21 6x2 dx !

                 penyelsaian:

                            

Jadi, hasil dari ʃ21 6x2 dx adalah 14.

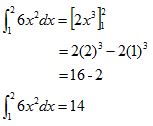
3. Integral Parsial                                                                                                         

Integral Parsial adalah suatu cara untuk menaikan pangkat suatu bilangan dua perkalian fungsi yang berbeda sehingga fungsi bilangan tersebut dapat menaikan pangkatnya (diintegralkan). Integral parsial dihubungkan dengan fungsi bilangan (u) dan (dv) yang fungsi tersebut akan dikali dan diintegralkan sesuai dengan aturan rumus integral parsial. Integral Parsial memiliki cara khusus dimana dua bilangan fungsi dari (u) dan (dv) akan dihitung untuk mencari penurunan pangkat dari (u) atau biasa disebut (du) dan mencari kenaikan pangkat (dv) atau biasa disebut (v).

Rumus umum :

                            ∫ u.dv = u.v - ∫ v.du

Keterangan :

Dengan (u) sebagai F(x) dan (du) sebagai F(x)'. Dan untuk fungsi (v) dan (dv) dalam soal kita memilih fungsi (dv) dengan syarat (dv) diintegralkansehingga membentuk (v). Setalah menemukan turunan (u) menjadi (du)dan integral (dv) menjadi (v). Nilai akan siap dimasukan ke dalam rumus integral parsial 

contoh: 
Berapakah hasil dari ∫ (3x + 2) sin (3x + 2) dx :
penyelsaian:

Maka

u = 3x + 2

dv = sin (3x + 2) dx

du = 3 dx

v = ʃ sin (3x + 2) dx = − ⅓ cos (3x + 2)

Sehingga

∫ u dv = uv − ∫v du

∫ u dv = (3x + 2) . (− ⅓ cos (3x + 2)) − ∫ (− ⅓ cos (3x + 2)) . 3 dx

∫ u dv = − (x+2/3) . cos (3x + 2) + ⅓ . ⅓ sin (3x + 2) + C

∫ u dv = − (x+2/3) . cos (3x + 2) + 1/9 sin (3x + 2) + C

Jadi, hasil dari ∫ (3x + 2) sin (3x + 2) dx adalah − (x+2/3) . cos (3x + 2) + 1/9 sin (3x + 2) + C.

4.    Integral Substitusi

Integral Substitusi juga merupakan salah satu teknik penyelesaian integral. Untuk menentukan ∫ f(x) dx, kita dapat mensubstitusikan u = g(x), dengan g fungsi yang dapat diintegralkan. Apabila substitusi itu mengubahf(x) dx menjadi h(u) du dan apabila H sebuah anti turunan dari h, maka kita dapat menotasikannya sebagai berikut : 

Misalkan : u = x - 1  maka  x = u + 1

$\frac{du}{dx}$ = 1   ⇔   du = dx

Contoh
$\begin{array}{cc}\int x(x-1{)}^{3}dx& =\int (u+1)u^{3}du\\ & =\int (u^4+u^3)du\\ & =\frac{1}{5}{u}^5+\frac{1}{4}{u}^4+C\\ & =\frac{1}{20}(4u^5+5u^4)+C\\ & =\frac{1}{20}(4u+5)u^4+C\\ & =\frac{1}{20}\left(4\right(x-1)+5)(x-1{)}^4+C\\ & =\frac{1}{20}(4x+1)(x-1{)}^4+C\end{array}$