CONTOH SOAL PERSAMAAN DIFERENSIAL EKSAK

Jawab
Langkah 1
buktikan persamaan differensial eksak.
M=3x2+4xy dan N=2x2+2y
Berarti,
∂M/∂y = 4x
Karena sama, maka PD ini EKSAK.
Selanjutnya, ambillah F(x,y)=C1, yang merupakan fungsi konstan. Berdasarkan bentuk (3x2+4xy)dx+(2x2+2y) dy, diketahui
∂F/∂x = 3x2+4xy ......(1)
dan
∂F/∂y = 2x2+2y..........(2)
F = x3+2x2y+ψ(x,y)
Turunkan F ini secara parsial terhadap y, diperoleh
∂F/∂y = 2x2+ψ′(x,y)
ψ′(x,y) = 2y ⇔ ψ(x,y) = y2 + C2. Jadi,
F=x3+2x2y+y2+C2=C1
M = 5xy+4y2
N = x2+2xy
sehingga hasil turunan parsialnya adalah
∂M/∂y = 5x+8y
Karena ∂M/∂y ≠ ∂N/∂x, maka persamaan diferensial ini tak eksak.
P(x) =1/N ( ∂M/∂y − ∂N/∂x )
P(x) =1/x2+2xy (5x+8y − (2x+2y) )
e∫3x dx = e3lnx = elnx3 = x3
Kalikan faktor integrasi ini ke (1) untuk mendapatkan
M=5x4y+4x3y2+x3
N=x5+2x4y
Jika kita menurunkan secara parsial M terhadap y dan N terhadap x, diperoleh
∂M/∂y = 5x4+8x3y
∂N/∂x = 5x4+8x3y
Karena sama, maka PD ini eksak.
Misalkan F= C0 (fungsi konstan). Telah diberikan
∂F/∂x = 5x4y+4x3y2+x3 ……(1)
dan juga
∂F/∂y=x5+2x4y ……(2)
Integrasikan (1) secara parsial terhadap x, diperoleh
F = x5y+x4y2+14x4+ϕ(y)
Lanjutkan: turunkan parsial kembali F ini tapi terhadap y, diperoleh
∂F∂y=x5+2x4y+ϕ′(y)
Bandingkan dengan (2), sehingga didapat bahwa
ϕ′(y)=0⇒ϕ(y)=C1
Berarti, solusinya adalah
F=x5y+x4y2+14x4+C1=C0
atau disederhanakan menjadi
x5y+x4y2+14x4=C

Jawab
Langkah 1
buktikan persamaan differensial eksak.
Nilai di atas = 0,
maka persamaan differensial diatas merupakan persamaan
Langkah 2
Selesaian PD di atas
adalah
F(x,y) = C. Untukmendapatkan F(x,y) = C dapat digunakan kesamaan:
2. (
x + 2y ) dx + ( 4y + 2x ) dy = 0
Jawab
Langkah 1
buktikan persamaan
differensial eksak.
Nilai di atas = 0,
maka persamaan differensial diatas merupakan persamaan
Langkah 2
Selesaikan PD di atas
adalah F(x,y) = C. Untuk mendapatkan
F(x,y) = C dapat digunakan kesamaan:
3. Tentukan solusi dari (3x2+4xy) dx+(2x2+2y) dy=0
Penyelesaian :
Bentuk persamaan
diferensial di atas merujuk pada persamaan diferensial eksak. Oleh karena itu,
kita periksa terlebih dahulu apakah ini PD eksak atau bukan.
Dari bentuk (3x2+4xy) dx+(2x2+2y) dy=0
Dari bentuk (3x2+4xy) dx+(2x2+2y) dy=0
kita misalkan bahwa
M=3x2+4xy dan N=2x2+2y
Berarti,
∂M/∂y = 4x
dan
∂N/∂y = 4x
Karena sama, maka PD ini EKSAK.
Selanjutnya, ambillah F(x,y)=C1, yang merupakan fungsi konstan. Berdasarkan bentuk (3x2+4xy)dx+(2x2+2y) dy, diketahui
∂F/∂x = 3x2+4xy ......(1)
dan
∂F/∂y = 2x2+2y..........(2)
Integrasikan (1) secara parsial terhadap x, diperoleh
F = x3+2x2y+ψ(x,y)
Turunkan F ini secara parsial terhadap y, diperoleh
∂F/∂y = 2x2+ψ′(x,y)
Bandingkan dengan (2), dan kita dapatkan bahwa
ψ′(x,y) = 2y ⇔ ψ(x,y) = y2 + C2. Jadi,
F=x3+2x2y+y2+C2=C1
x3+2x2y+y2=C dengan C = C1 − C2
Jadi,
penyelesaiannya adalah x3+2x2y+y2=C
4. Tentukan
penyelesaian dari (5xy+4y2+1) dx+(x2+2xy) dy = 0
Penyelesaian :
Diberikan PD (5xy+4y2+1) dx+(x2+2xy) dy=0……(1)
Langkah pertama adalah memeriksa apakah persamaan diferensial di atas eksak atau tidak.
Misalkan:
Langkah pertama adalah memeriksa apakah persamaan diferensial di atas eksak atau tidak.
Misalkan:
M = 5xy+4y2
N = x2+2xy
sehingga hasil turunan parsialnya adalah
∂M/∂y = 5x+8y
∂N/∂x = 2x+2y
Karena ∂M/∂y ≠ ∂N/∂x, maka persamaan diferensial ini tak eksak.
Agar eksak, kita harus mencari faktor integrasi terlebih dahulu.
Faktor integrasinya berbentuk e∫P(x) dx
Faktor integrasinya berbentuk e∫P(x) dx
P(x) dapat
dicari dengan menggunakan cara berikut.
P(x) =1/N ( ∂M/∂y − ∂N/∂x )
P(x) =1/x2+2xy (5x+8y − (2x+2y) )
P(x) =1/x2+2xy (3x + 6y))
P(x) = 3x(x+2y(x+2y)) =3/x
P(x) = 3x(x+2y(x+2y)) =3/x
Karena P(x) hanya
bergantung terhadap variabel x (sesuai
persyaratan metode PD tak eksak), maka kita dapatkan faktor integrasi
e∫3x dx = e3lnx = elnx3 = x3
Kalikan faktor integrasi ini ke (1) untuk mendapatkan
x3(5xy + 4y2 + 1) dx + x3( x2 + 2xy) dy=x3⋅0
(5x4y + 4x3y2 + x3) dx+(x5+2x4y) dy
= 0
Misalkan
M=5x4y+4x3y2+x3
N=x5+2x4y
Jika kita menurunkan secara parsial M terhadap y dan N terhadap x, diperoleh
∂M/∂y = 5x4+8x3y
∂N/∂x = 5x4+8x3y
Karena sama, maka PD ini eksak.
Misalkan F= C0 (fungsi konstan). Telah diberikan
∂F/∂x = 5x4y+4x3y2+x3 ……(1)
dan juga
∂F/∂y=x5+2x4y ……(2)
Integrasikan (1) secara parsial terhadap x, diperoleh
F = x5y+x4y2+14x4+ϕ(y)
Lanjutkan: turunkan parsial kembali F ini tapi terhadap y, diperoleh
∂F∂y=x5+2x4y+ϕ′(y)
Bandingkan dengan (2), sehingga didapat bahwa
ϕ′(y)=0⇒ϕ(y)=C1
Berarti, solusinya adalah
F=x5y+x4y2+14x4+C1=C0
atau disederhanakan menjadi
x5y+x4y2+14x4=C
Terima Kasih


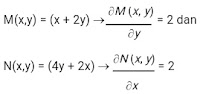

Komentar
Posting Komentar